인공지능 플래닝

AI 개념과 에이전트

AI 개념

ai

• 사람처럼 생각한다. - thinking humanly
• 계산적인 모델을 통해 지능을 연구 - thinking rationally
• 사람이 더 나아지는 방향으로 컴퓨터를 만드는 연구 - acting humanly
• 지능적으로 행동한다 - acting rationally

튜링 테스트

• 기계가 생각 가능한가? → 기계가 지적으로 행동할 수 있는가?
• 반복 불가. 수학적인 분석으로 수정하거나 생성할 수 없다.

사람처럼 생각하기(thinking humanly) - cognitive science(인지과학)

• 행동 관점과 상반된 주장에서 나왔다. 심리학에 가깝다.
• 뇌의 내부 행동의 과학적 이론이 필요하다.
  • 추상화의 단계는? Knowledge or Circuits
  • How to validate?
    • 사람의 행동을 예측하거나 테스트한다. (탑다운)
    • 뇌과학적인 지능으로 부터 직접 명령한다.(바텀업)
  • 예를 들어 사람의 정신에 대한 충분한 정보와 이론을 얻어 프로그램을 짰다고 가정할때, 프로그램의 입출력이 인간의 행동과 부합하면 일부 메커니즘이 인간적으로 작동한다고 볼 수 있다.

이성적으로 생각하기(thinking rationally) - Laws of Thought

• descriptive(서술적) 보단 사전에 정한 규칙대로 진행한다. - 아리스토텔레스의 삼단논법
• 생각의 틀을 잡고 선을 정하는게 현대 AI 발전의 길이다.
• 문제점
  • 모든 informal 지식을 formal 용어로 표현하기 어렵다.
  • 모든 지능적 행동이 logical deliberation에 따르지 않는다. → 추론 단계에 따라 문제가 풀리지 않을 수 있다.

사람처럼 행동하기

• 사람이 행동하는 것을 따라한다.
• 사람이 더 잘하는 것을 컴퓨터가 할 수 있게 만든다.

사람처럼 행동하기(인간적 행위) - 튜링 검사 접근방식

• 튜링검사 - 사람처럼 대답한다.
• 자연어 처리 - 사람과 의사소통이 되게 한다.
• 지식 표현 - 알고 & 들은 정보를 저장한다.
• 자동 추론 - 정보를 이용해 질문에 답하고 새로운 결론을 도출한다.
• 기계 학습 - 기존의 정보를 새로운 상황에 사용할 수 있게 한다.
• 완전 튜링 검사 - 물리적 시뮬레이션이 포함된 튜링 검사(비디오 신호가 포함된다). 두 조건이 충족해야 한다.
  • 컴퓨터 비젼
  • 로봇공학

이성적으로 행동하기

• 올바른 것을 한다.
• The right Thing - goal achievement을 최적화하는 방향
• 생각을 꼭 수반하지 않는다. (eg. 눈 깜박이기) 하지만, 있으면 좋다.

이성적으로 행동하기 - 이성적인 에이전트 접근방식

• 입력과 출력이 있는 하나의 객체다.
• 자율적으로 작동하고 환경을 인지하고, 장기간 행동을 유지하고, 변화에 적응하고, 목표를 만들고 추구한다.
• rational agents를 디자인하는 것이 ai 플래닝의 목표
• 핵심: 받아들인 축적된 histories를 행동으로 변환하는 함수(기능)
• 주어진 다양한 환경과 task로 부터 최고의 성능을 추구한다.
• 튜링 검사 통과에 필요한 능력이 이성적인 에이전트를 만드는데 도움이 된다.

에이전트

PAGE

• Percepts: 재료와 같은 입력. 받아들인 지각
  • 에이전트는 지각하지 못한 것에는 전혀 의존하지 않는다.
• Actions: 재료로 만든 행동
• Goals: 행동으로 진행할 목표
• Environment: 주변 환경

Rational agents(전지전능한x, 천리를 보는x, 성공을 추구하는x)

• 이성적인 에이전트는 omniscient를 추구하지 않는다. omniscient는 완벽함을 추구한다. 하지만 에이전트는 percept sequence에 의존해 최적의 행동을 도출한다.
• 합리성. 합리성은 네가지 요소가 필요하다.
  • 성과 측정 - 성공의 기준을 정의한다.
  • 환경에 대한 에이전트의 사전 지식
  • 에이전트가 수행할 수 있는 동작들
  • 에이전트의 지금까지의 지각열(given the percept sequence to date)
• 즉, 합리적 에이전트는 percept sequence와 사전 지식으로 성과 측정치를 극대화하는 동작을 선택한다. (주어진 percept sequence로 성과 측정의 기댓값을 최대화해야한다.)

문제 해결 설정

Environment types

• inaccessible
• stochastic - deterministic or stochastic
• sequential - episodic or sequential
• dynamic - static or dynamic. 환경 자체는 변하지 않지만 에이전트의 결정에 따라 성과 측정치가 변하는 경우: semidynamic
• continuous - discrete or continuous
• unknown - known or unknown. 에이전트의 지식 상태에 관한 구분. environment type은 아님.
  • known이 fully observable만은 아니다. partial observable도 존재한다. - solitaire에서 모든 규칙을 알지만 뒤집지 않은 카드의 정보는 알 수 없다.
  • unknown이 partial observable만은 아니다. fully observable도 존재한다. - 비디오 게임 첫 화면에서 모든 버튼의 동작을 알지 못하지만 게임 화면의 모든 정보는 알 수 있다.

Problem types

참고.

• 관찰 가능하다 → fully observable
• 부분 관찰이 가능하다 → partial observable
• fully observable X, deterministic X(stochastic) → Uncertain
• 결정가능한, 접근가능한(single-state problem)
• 결정가능한, 접근불가능한-정보를 다 모르는(mulitiple-state problem)
• 결정불가능한, 접근불가능한(contingency problem-대책이 필요한 문제)
  • 실행동안 센서를 사용해야한다.
  • tree 방식이나 policy 방식을 사용한다.
• Unknown(infinite) state space(exploration problem-온라인 문제. 얼마나 많은 데이터, state가 나올지 모르는.)

Agent functions and programs

• 에이전트는
  • percept 후 메모리에 업데이트
  • 메모리에서 최고의 액션을 선택
  • 메모리 최적화

Skeleton Agent

여러가지 에이전트

Agent types

• simple reflex agents
• reflex agents with state
• goal-based agents(목표 달성을 지향한다)
• utility-based agents(목표 달성에 지름길을 활용한다) - optimal(최적화. 얼마나 searching을 잘하는가)

Simple reflex agents

• sequence는 고려하지 않고 현재 percept만 고려한다.
• 즉, 완전 관찰 가능(fully observable)에서만 작동한다.
• 따라서 무한 루프에 빠질 가능성이 있다. eg. 위치감지기가 없는 진공청소기(partial observable). left 상태에서 left로 이동하려고 하는 경우(갈 수 있는 칸이 ㅁㅁ 이렇게 되어 있다고 가정할 때).
  • 무작위화(randomization) 개념을 넣으면 해결 가능하다.
    • 다중 에이전트에서 무작위화는 도움이 될 때가 있다.
    • 단, 단일 에이전트에서 무작위화는 대체로 합리적 이지 않다.
• 조건-동작 규칙(condition-action rule)이다.
• 우리의 간단한 생리적 행동을 생각하자. eg. 뜨거운 물체를 잡았을때, 바로 손을 뗀다. 앞차가 제동을 걸면 나도 제동을 건다.

1. percept를 바탕으로 현재 state를 추측
2. state(eg. finite state machine)에 맞는 rule을 매칭
3. rule에 해당하는 action 리턴

• 진공청소기 환경 단순 반사 에이전트 - left, right, suck, do nothing

Reflex Vacuum Agent

Reflex agents with state(model-based agent)

Reflex agents with state

• partial observable 가능성을 해결한다.

1. percept를 받아 현재 state 추측
2. model은 action에 영향을 받은 state가 어떻게 될지 추측
3. 추측한 state 반영
4. state에 해당하는 rule 매칭
5. rule에 해당하는 action 리턴

Goal-based agents

• 에이전트의 내부 상태뿐만 아니라 목표를 설정한다.
• 목표를 달성하기 위한 action sequence를 찾아야한다.
  • search, planning이 이를 가능하게 한다.

Goal-based agents

Utility-based agents

• 목표 + 효용. 더 나은 방향으로 목표를 수행하게 한다.
• utility function이 내장되어 있다.
  • utility function과 외부 성과 측정 사이에 모순이 없다면 효용을 최대화하는 방향으로 동작한다.
• expected utility를 최대화하는 방향으로 동작한다.

Utility-based agents

문제 해결과 검색

문제 해결과 검색(Problem solving and search)

• problem-solving 에이전트는 목표 기반 에이전트의 하나이다.
• 세계의 상태를 episodic으로 간주한다.
• uninformed 검색 알고리즘은 어떠한 문제라도 풀 수 있으나 효율적으로 풀지는 못한다.
• informed 알고리즘은 효율적으로 문제를 풀 수 있다.

문제 해결 에이전트

Problem-solving agent

• 문제 해결 에이전트는 목표를 정하고 성과 측정치를 최대화한다.
• 목표와 성과 측정치에 집중하기 때문에 의사결정 문제가 간단해진다.
• 따라서 고려해야할 동작들이 제한된다. eg. 환불 불가 비행기 티켓으로 떠날때, 여행지에 도착하는 것이 목표이기 때문에 제때 도착하지 못하는 것은 배제한다.
• 이러한 goal formulation(목표 형식화)와 problem formulation(문제 형식화)가 중요하다.
• action sequence를 찾는 공정 - search. action sequence - solution. execution
• formulation → search → execution의 단계로 설계한다.

전형적인 problem-solving agent

Simple Problem Solbing Agent

1. percept를 받아 현재 state 추측
2. action sequence가 없다면
   1. state로 goal formulate를 한다.
   2. state와 형식화된goal로 problem formulate를 한다.
   3. 형식화된 문제에 대한 action sequence를 찾는다(search).
   4. action sequence가 failure이면 동작하지 않는다.
3. action sequence에서 첫번째 action을 수행하고 그 action을 action sequence에서 제거한다.
4. 루프를 반복한다.

1. solution: 5 → 6 → 8
2. 시작점이 1~8 모두 가능.
3. solution: 1→5→6→8. 2→4→3→7
4. 5번에서 현재 위치에 먼지가 없어 할일이 없음. suck이 되려 더러워지게 할 수 있기 때문에
5. 센서를 활용하면(partially observable이기 때문에), 5 → 6 → 8

Example: vacuum world

싱글 state 문제

• 상태 공간(state space)
  • initial state
  • operators(sequence of actions)
  • 전이모형(transition model). eg. RESULT(In(Arad), Go(Zerind) = In(Zerind)
• goal test
• path cost(경로에 따른 비용)
• initial state → goal state 로 갈때까지 과정이 반복된다.
• 그중 최적해(optimal solution)을 찾는다. 이는 sequence of operators이다.

state space 설정

• 문제 해결을 위해 state space를 추상화한다.
• (Abstract)state - 실제 상태 중 일부
• (Abstract)operator - 실제 actions의 복합적인 작용
• (Abstract)solution - 실제 세계에서 솔루션을 향한 실제 경로의 일부
• Abstract도 실제와 같다고 볼 수 있다. 보다 easier을 위해 추상화한것

검색 알고리즘

일반적인 검색 알고리즘

Search algorithm(Search Tree)

• 구조
  • n: 현재 노드
  • n.state: 노드에 해당하는 상태
  • n.parent: 부모 노드
  • n.action: 부모 노드에서 현재 노드가 되기 위해 행한 것
  • n.path-cost: 루트 노드에서 현재 노드까지의 비용(경로)
  • node와 state는 다르다. 서로 다른 두 노드가 같은 상태를 가질 수 있다. 따라서 이러한 노드들을 저장해줄 queue(대기열)이 필요하다.
• 결과는 하나의 동작열(action sequence)이다.
• 초기 상태에서 시작하는 가능한 action sequence는 하나의 검색 트리(search tree)를 형성한다.
  • tree의 구성 요소
    • root: initial state. branch: action. node: state
  • tree 성장 과정
    1. initial state가 goal state인지 확인한다.
    2. state에 action을 한 다음 state를 생성 및 확장한다. 여기서 state는 frontier node이다.
  • Tree search 알고리즘
  • Graph search 알고리즘
    • 탐색집합을 추가해 과잉 탐색을 막는다.
     

Tree-Search

Search Algorithms

State vs Node

• state는 물리적인 구성의 하나이다.(real한 것)
• node는 search tree의 구조적 구성의 하나이다.(state를 컴퓨팅적으로 표현한 것)
• 즉, parent, children, depth와 같은 tree 구성의 특징은 node만 있다.
• 우리는 state를 표현하기 위해 node를 활용한다. 점차 node를 확장시켜 실세계와 가까운 것을 만든다.

문제 해결 성능 측정

• Strategy 평가 요소
  • 완결성(completeness): 문제에 해답이 존재할 때, 알고리즘이 반드시 해답을 찾아내는가
  • 최적성(optimality): 검색 전략이 최적해를 찾아내는가
  • 시간 복잡도(time complexity): 해답을 찾는데 얼마나 시간이 걸리는가
  • 공간 복잡도(space complexity): 검색을 수행하는데 메모리가 얼마나 필요한가
  • 분기 계수(branching factor): 임의의 노드의 후행자 최대 개수
  • 깊이(depth): 목표 노드의 깊이
  • 길이(maximum length): 상태 공간 임의의 경로의 최대 길이
   

문제 해결 성능 측정

Uninformed Search Strategies

Uniformed search strategies

• 상태에 관해 문제 정의 이상의 정보를 제공받지 못하는 상황
  • 따라서 할 수 있는 일은 후행자들을 생성하고 목표 상태와 비목표 상태를 구분해야 하는 것이다.
  • 어떤 비목표 상태가 더 유망한지 판단하는 전략은 informed search에서 다룬다.
• Breadth-first search(너비 우선 탐색)
  • Queue를 활용한다. frontier은 전선이다.
  • 깊이가 얕은 노드부터 탐색한다.
  • 목표 판정을 확정할 노드를 생성할 때 수행한다.
  • 성능 측정
    • 완결성: 완결적이다. (목표 노드가 유한한 깊이에 있을 때)
    • 시간 복잡도: O(b^d), (b: 후행자 노드 개수, d: 목표 노드까지의 깊이. 노드를 선택할 때 목표 판정을 하면 d+1이 된다.)
    • 공간 복잡도: O(b^d), (탐색한 노드 집합은 O(b^(d-1)), 전선 노드 집합은 O(b^d))
    • 최적성: 항상 최적해는 아니다. 경로 비용이 노드 깊이에 비감소 함수 일 때, 최적이다.
      • 비감소 함수가 아니라면 BFS는 최적해가 아닌 가장 비싼 경로를 반환할 수도 있다.
    • BFS는 시간복잡도보다 공간복잡도(메모리 요구량)이 큰 문제이다.
    • 하지만 시간 역시 큰 문제이다.(둘다 기하급수적으로 늘어나기 때문.)
    • 1초에 100만 노드 생성 가능. 1 노드 당 1000바이트라고 가정.
    • 1초에 1기가 바이트 필요. 깊이가 10인 문제는 3시간이 걸리며, 10 TB가 필요하다.
     

Breadth First Search Algorithm

Breath First Search Algorithm 성능

• Uniform-cost search(균일 비용 검색)
  • BFS에서 경로 비용을 고려한 알고리즘(단계 비용 함수에 최적해를 찾기 위한 알고리즘)
  • 경로 비용 g(n)에 대해 정렬한 뒤, g가 가장 낮은 노드 n을 확장한다.
    • g(n) = 경로까지의 모든 비용의 합
  • BFS와의 차이점
    • 경로 비용 g(n)에 따라 정렬한다.
    • 목표 판정은 확장을 위해 선택될 때 수행한다.
    • 경로 비용이 더 나은 노드가 있는지 판단한다.
  • 루마니아 상태 공간 예시
    • 시비우 → 부카레스트
    1. 비용이 더 싼 림니쿠 빌차(80) 노드를 확장한다.
    2. 80 + 97 = 177인 피테스티 노드가 추가된다.
    3. 피테스티(177)보다 비용이 더 싼 파가라스(99) 노드를 확장한다.
    4. 99 + 211 = 310인 부카레스트 노드가 추가된다.
    5. 목표 노드인 부카레스트가 생성됐지만, 최적해를 판단하기 위해 피테스티 노드를 확장한다.만약, BFS처럼 INSERT 전에 목표 노드인지 판단한다면 더 나은 비용의 최적해를 찾을 수 없다.
    6. 80 + 97 + 101 = 278인 부카레스트의 또 다른 경로를 추가한다.
  • 성능 측정
    • 완결성: 완결적이다. (경로 비용이 작은 양의 상수 ε보다 클때)
    • 시간 복잡도, 공간 복잡도: 노드 수(b)나 깊이(d)가 아닌 비용으로 판단해야 한다.작은 단계들을 모두 지난 뒤, 큰 단계를 지나는 경우이다.
    • 모든 경로 비용이 동일할 때, O(b^(d+1))이다. 즉, 이 경우, BFS보다 나쁘다.
    • 최적해의 비용이 C*이고, 모든 동작의 비용이 적어도 ε일 때, 최악의 경우 O(b(1+C/ε))이다.
    • 최적성: 항상 최적해이다.
     

Uniform Cost Search Algorithm

Uniform Cost Search Algorithm 성능

• Depth-first search
  • Queue가 아닌 Stack을 사용한다.
  • 성능측정
    • 완결성:
      • 그래프 검색: 완결적이다. 그래프 검색은 반복과 과잉 경로를 피하기 때문이다.
      • 트리 검색: 완결성을 보장할 수 없다. 무한 루프에 빠질 수 있기 때문이다.
        • 내가 지나온 길을 반복해서 도는 경우, 깊이가 무한대인 경우
    • 시간 복잡도: O(b^m)
      • 그래프 검색: 상태 공간 크기에 따라 상계와 하계가 존재한다.
      • 트리 검색: 최악의 경우, 검색 트리의 모든 노드를 생성할 수 있다.
    • 공간 복잡도: O(bm), (b: 후행자 노드 개수, m: 노드의 최대 깊이). —> DFS의 장점
    • 한 노드를 확장 하고 그 모든 후손을 완전히 탐색했다면 해당 노드를 메모리에서 제거한다.
    • 최적성: 최적의 해가 아니다.
      • 목표 노드가 A, B이고 A가 왼쪽 부분 트리, B가 오른쪽 부분 트리이며 최적해라고 가정하자.
      • DFS는 A를 해답으로 반환한다.
  • 일련의 문제를 백트래킹을 활용해 해결이 가능하다.

Depth First Search Algorithm 성능

• Depth-limited search
  • DFS의 문제점을 깊이 제한을 두어 해결한 알고리즘
  • 깊이 제한(l)을 두어 무한 경로 문제를 해결한다.(무한 루프에 빠지는 경우)
  • l < d 일 때, 문제는 완결되지 않는다.(깊이 제한 보다 목표 노드의 깊이가 더 깊을 때)
  • 성능 측정
    • 완결성: 완결적이지 않다.(l < d 일 때)
    • 시간 복잡도: O(b^l)
    • 공간 복잡도: O(bl)
    • 최적성: 최적의 해가 아니다.(l < d 일 때)
  • 가능한 l의 범위를 잘 설정하면 최적의 상황 조성이 가능하다. 이는 지름(diameter)을 잘 설정하는데 달려있다.
    • 문제에 대한 지식을 가지고 있을 때 가능하다.
  • 두가지의 실패 경우가 존재한다.
    • failure: 해답이 없다.
    • cutoff: 주어진 깊이 한계 내에서 해답이 없다.
     

Depth-limited search Algorithm

• Iterative deepening search
  • 최상의 깊이 한계를 찾는 알고리즘이다.
  • DFS 트리와 함께 사용한다.
  • 깊이 한계를 점차 증가시켜 가장 얕은 목표 노드 d를 발견하는 게 목표다.
  • DFS + BFS 장점을 합친 버전이다.
  • 분기 계수가 유한할 때 완결적이다.
  • 경로 비용이 노드 깊이의 비감소 함수일 때 최적이다.
  • 성능 측정
    • 완결성: 완결적이다. (분기 계수가 유한할 때 → BFS와 같음)
    • 공간 복잡도: O(bd). (→ DFS와 같음)
    • 시간 복잡도: O(b^d)
      • 최하위(d) 노드는 한번 생성되고, 그 위 노드들은 반복해서 생성된다.
    • 최적성: 최적의 해이다. (경로 비용이 노드 깊이의 비감소 함수일 때 → BFS와 같음)
  • 일반적으로 검색 공간이 크고 해답의 깊이가 알려지지 않을 때 사용한다.

Iterative deepening search Algorithm

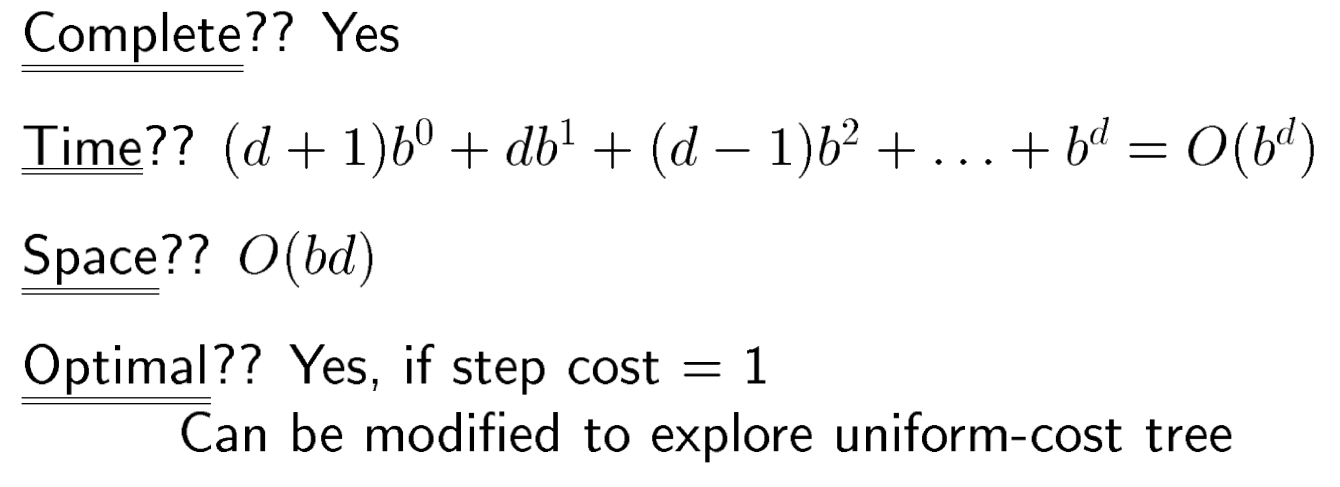
• Bidirectional Search(양방향 검색)
  • 초기 상태에서 시작하는 전방 검색과 목표에서 시작하는 후방 검색을 동시에 수행한다.
  • b^(d/2) + b^(d/2) < b^d 의 이점을 가진다.
  • 두 검색의 전선이 교차해야 해답이 존재한다.
  • 성능 측정
    • 시간 복잡도: O(b^(d/2)). (2*b^(d/2)는 O(b^(d/2)이다)
    • 공간 복잡도: O(b^(d/2)). (2*b^(d/2)는 O(b^(d/2)이다)
      • 둘 중 하나에 반복 심화를 적용한다면 대략 절반으로 줄일 수 있다. → b^(d/2) + b(d/2)가 된다.
      • 단, 교차 판정을 위해 두 전선 중 적어도 하나는 메모리에 유지해야 한다.
    • 공간 요구량이 가장 큰 약점이다.
  • 후방 검색을 위해 역방향으로 검색하는 방법을 알아야하는 문제점이 있다.
    • 선행자(predecessor)를 찾는 것은 어렵다.

Informed Search

• Best-First Search
  • 트리 검색이나 그래프 검색 알고리즘
  • 균일 비용 검색과 알고리즘이 같되 g(n)이 아닌 f(n)으로 경로를 판단한다.
  • 확장할 노드를 평가 함수(evaluation function - f(n))에 기초해 선택한다. f(n)이 가장 낮은 노드가 먼저 확장된다.
  • f(x)의 선택은 검색 전략을 결정한다. 대부분의 f에는 heuristic이 포함된다.
  • 각 노드마다 heuristic(desirability) - h(n)을 계산한다.
    • h(n) = 노드 n에서 목표 상태로의 가장 싼 경로 추정 비용(직선 거리)
    • h(n) > 0, 목표 노드의 h(n) = 0
  • greedy search와 A*알고리즘이 특이 케이스

Best-First Search

• Greedy-First Search
  • f(n) = h(n)
  • 각 노드마다 heuristic을 계산한다.
  • heuristic은 현재 노드와 goal 노드간 직선 거리
  • heuristic이 가장 작은 값을 따라간다.
  • 성능 측정:
    • 완결성: 완결적이지 않다.
      • 이아시 → 파가라스일 때, 그리디 알고리즘은 네암트를 확장한다. 그럼 막다른 길에 도착해 목표 노드까지 갈 수 없다. 무한 루프에 빠진다.
      • 그래프 검색에서는 유한한 공간에서 완결적이다.
    • 시간 복잡도: O(b^m)
    • 공간 복잡도: O(b^m)
    • 최적성: 최적의 해가 아니다. 매 단계마다 가장 싼 값을 고르기 때문에 전체적으로 최적인 해를 구하지는 않는다.

Greedy-First Search

Greedy-First Search 성능

• A* 알고리즘
  • 이미 방문한 경로는 피한다.
  • 가능성이 없는 노드는 확장하지 않는다. → prunning(가지치기)
  • Optimally efficient하다. A*보다 더 적은 노드를 확장하는 최적의 알고리즘은 없다.
  • f(n) = g(n) + h(n)(그리디 + 휴리스틱(desirability) 알고리즘. h는 partial observable 요소이다.)
    • f(n) = n을 거쳐 가는 가장 싼 해답의 추정 비용
    • g(n) = 경로까지 모든 비용의 합
  • 알고리즘은 균일 비용 검색 알고리즘과 같되 g(n) 대신 g(n) + h(n)으로 한다.
  • 성능 측정
    • 완결성: 완결적이다.
      • 단, 비용이 C*(최적해 경로 비용) 이하인 노드가 유한해야한다.
    • 최적성: 최적의 해이다.
    • 시간 복잡도 —- 질문: 각각의 경우에 따라 복잡도가 왜 다른지
      • 절대오차 Δ ≡ h* -h. 상대오차 ε ≡ (h* - h) / h*
      • 목표가 하나이며, 동작이 가역적인 경우: O(b^Δ)
      • 단계 비용들이 일정한 경우: O(b^(εd)) = O((b^ε)^d). (d는 해답의 깊이)
        • 즉, 유효 분기 계수는 b^ε이다.
        • d에 지수적이다.
    • 공간 복잡도: 모든 노드를 메모리에 저장해야한다.(모든 그래프 검색 알고리즘이 그러하다.)
    • 최적성 요건 - 트리 검색
      • 허용 가능 발견법적 함수(admissible heuristic) → h(n)을 과도하게 설정하지 않는다.
        • f(n) = g(n) + h(n)은 항상 최소 경로를 찾아야한다(최적해를 구하기 위해). 여기서 g(n)은 노드간 실제 거리이므로 상수이다.
        • h(n)에 대해 h(n) ≤ h*(n)이어야 한다. (h*(n)은 실제 거리 = 실제 최소 비용)
          • 위를 만족해야 f(n)이 항상 최소 경로를 찾는다고 보장할 수 있다.
        • 가장 명백한 예는 직선거리이다. 직선거리는 절대 실제 거리보다 과대추정될 수 없다.
      • 일관성(consistency), 단조성(monotonicity) - 그래프 검색 —- 질문: 내가 이해한 게 맞는지
        • h(n) ≤ c(n, a, n’) + h(n’), (n’: n에 a(action)을 행한 후행자, c: cost, c는 step 비용으로 볼 수 있다. 즉, 두 노드간 거리)
        • → c(n, a, n’)은 step 비용으로 상수값(c)이다. h(n)은 항상 실제 거리보다 작은 하계의 값으로 유동값이다. h(n) ≥ h(n’) + c라면, h(n)은 실제 거리 h*(n)을 넘어선 값이 된다.
  • 최적성 증명하기
    • h(n)이 일관적이면, 임의의 경로에 있는 f(n)의 값들은 비감소이다. —- 질문: uninformed에서 비감소여야하는 이유와 동일한가. 비감소여야 최적의 해를 구한다. 그 이유는 검색을 이어나가는 의미가 있기 때문
      • f(n’) = g(n’) + h(n’) = g(n) + c(n, a, n’) + h(n’) ≥ g(n) + h(n) = f(n). f(n’) ≥ f(n)
      • 나의 생각: 검색이 진행됨에 따라 최적의 경로에서 g는 증가하고 h는 감소한다.
    • A*가 확장을 위해 노드 n을 선택할 때, 그 노드로의 최적 경로가 이미 발견돼 있다.
      • 시작 노드를 중심으로 점차 비용이 증가하는 띠들의 형태로 노드를 추가한다. 옆 그림 참고
    • A는 f(n) < C인 모든 노드를 확장한다.
    • A는 목표 노드를 선택하기 전에 목표 등고선(f(n) = C인 등고선)에 걸쳐있는 일부 노드들을 확장할 수 있다.
   

부카레스트 경로 문제

• 문제점
  • 검색 공간 안의 상태의 수가 해답 길이 d에 지수적이다.
    • 최적해 깊이 d의 실행 시간 증가 정도를 절대오차 Δ와 상대오차 ε를 통해 분석한다.
    • 거의 모든 heuristic 함수들은 절대오차 Δ가 h*에 비례하므로 상대오차 ε은 상수이거나 증가한다.
    • 상태의 수가 d에 지수적인 만큼 시간 복잡도도 d에 지수적이다.
  • 목표 상태가 여러 개일 때, near-optimal이 여러 개일 때
    • 검색 공정이 최적 경로에서 멀어질 수 있다.
    • 목표 개수에 비례하는 추가 비용이 들 수 있다. 최적 비용의 1/ε 이내
  • 일반적인 그래프의 경우
    • f(n) < C*인 상태의 수가 지수적일 수 있다.
    • eg. 에이전트가 사각형을 청소한다. 더러운 사각형이 N개이다. 이때 f(n) < C*를 만족하는 상태들은 2^N개다.

• A* 알고리즘 변형
  • IDA*
    • A* 알고리즘의 메모리 요구량을 줄여준다.
    • 깊이 대신 g + h(비용)을 cutoff로 사용한다.
    • cutoff 설정은 이전 반복의 cutoff보다 크지 않은 가장 작은 값 f로 한다.
    • 단계 비용이 일정한 문제에 유용하다.
  • RBFS —- 추가
  • MA* —- 추가
  • SMA* —- 추가
  • 문제점
    • 검색 공간 안의 상태의 수가 해답 길이 d에 지수적이다.
      • 최적해 깊이 d의 실행 시간 증가 정도를 절대오차 Δ와 상대오차 ε를 통해 분석한다.
      • 거의 모든 heuristic 함수들은 절대오차 Δ가 h*에 비례하므로 상대오차 ε은 상수이거나 증가한다.
      • 상태의 수가 d에 지수적인 만큼 시간 복잡도도 d에 지수적이다.
    • 목표 상태가 여러 개일 때, near-optimal이 여러 개일 때
      • 검색 공정이 최적 경로에서 멀어질 수 있다.
      • 목표 개수에 비례하는 추가 비용이 들 수 있다. 최적 비용의 1/ε 이내
    • 일반적인 그래프의 경우
      • f(n) < C*인 상태의 수가 지수적일 수 있다.
      • eg. 에이전트가 사각형을 청소한다. 더러운 사각형이 N개이다. 이때 f(n) < C*를 만족하는 상태들은 2^N개다.
• A* 알고리즘 변형
  • IDA*
    • A* 알고리즘의 메모리 요구량을 줄여준다.
    • 깊이 대신 g + h(비용)을 cutoff로 사용한다.
    • cutoff 설정은 이전 반복의 cutoff보다 크지 않은 가장 작은 값 f로 한다.
    • 단계 비용이 일정한 문제에 유용하다.
  • RBFS —- 추가
  • MA* —- 추가
  • SMA* —- 추가
• heuristic 함수
  • Admissible Heuristic
    • eg. 8-퍼즐 문제
      • 평균 해답 비용 h* = 26
      • h1 = 잘못 놓여진 타일의 개수. (예시에서는 7개)
      • h2 = 맨해튼 거리 총합. (예시에서는 2 + 3 + 3 + 2 + 4 + 2 + 0 + 2 = 18칸)
      • h1, h2 모두 h*를 초과하지 않는다. admissible
  • 성능 요소
    • 유효 분기 계수(effective branching factor) b*가 중요하다.
    • A가 생성하는 전체 노드 개수가 N, 전체 해답 길이가 d일 때, N + 1 = 1 + b + (b*)^2 + … + (b*)^d 이다.
    • 잘 설계된 heuristic 함수는 b*가 1에 가깝다.
  • domination
    • h1(n) ≤ h2(n)은 자명하다. → 우세하다.
    • 증명
      • f(n) < C이므로 h(n) < C - g(n)인 모든 노드는 확장된다.
      • 모든 노드에 대해 h2가 h1보다 작지 않다.
      • 따라서 h2를 활용하는 A가 확장하는 노드는 h1을 활용하는 A에서도 확장된다.(h1이 더 많은 노드를 확장한다.)
• Relaxed Problem
  • 문제에 대해 제약을 완화한다. 이를 통해 더 나은 해답을 찾는다.
  • 검색없이 문제를 해결할 수 있다.
  • 8-퍼즐 문제에서 타일이 any where 갈 수 있다면, h1이 최단 해답을 제공한다.
  • 8-퍼즐 문제에서 타일이 any adjacent square로 갈 수 있다면, h2가 최단 해답을 제공한다.

8-퍼즐 문제

심화 검색 알고리즘

Local Search

Local Search

• 경로 비용은 중요하지 않고 해답 상태만 중요하다.
• current node만 사용한다. 경로는 저장하지 않는다.
• 장점
  • 메모리를 적게 소비한다.
  • infinite 상태 공간에서도 해답을 찾는다.
• Hill-Climbing Search
  • 값이 증가하는 방향으로 이동한다.
  • adjacent node에 증가하는 값이 없으면 탐색을 종료한다.
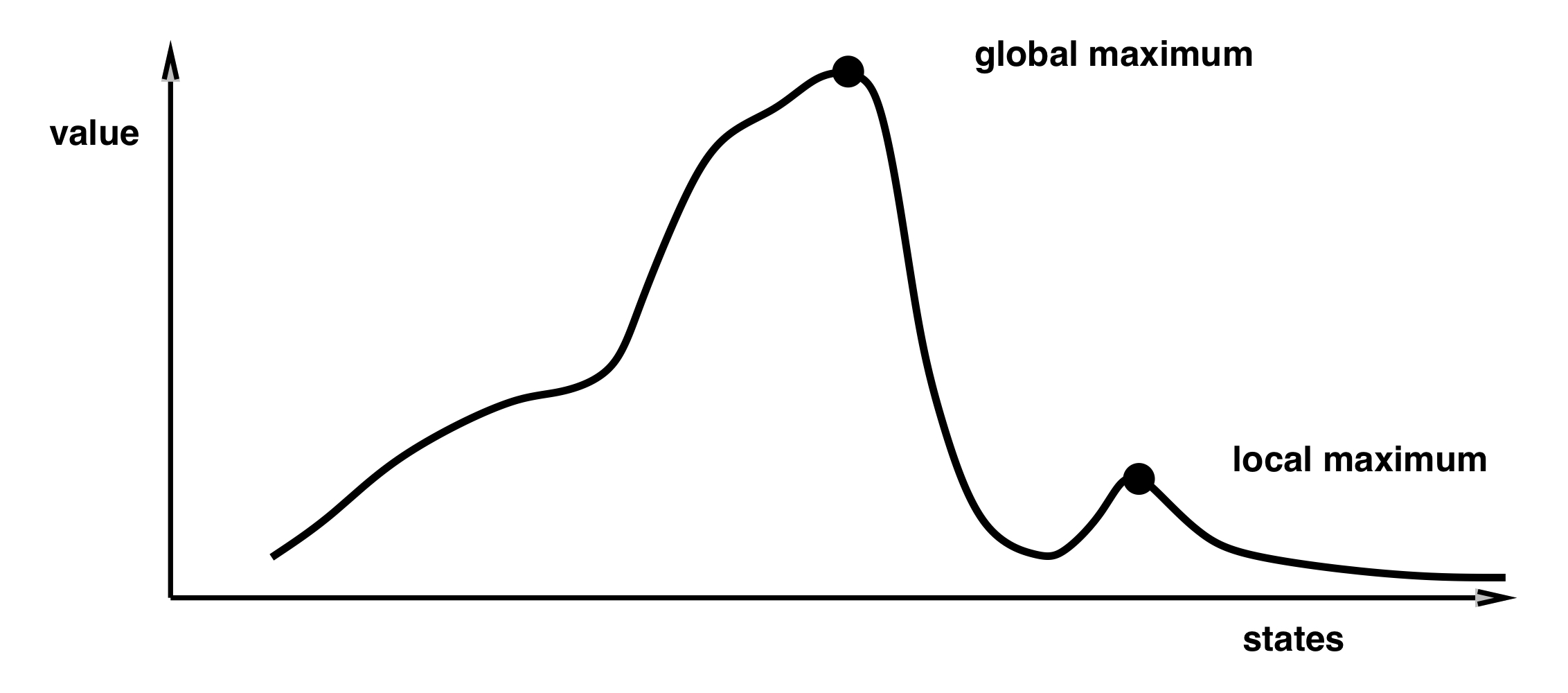
  • local maximun에 도달하면 더이상 이동하지 않는다. 즉, global maximum에 도달할 수 없다.
  • 또한 값이 동일한 상태인 shoulder에 위치하면 길을 잃는다.
• Simulated Annealing
  • Hill-Climbing Search는 local maximum에 머무를 수 있으므로 완결적이지 않다.
  • 탐색에서 다음과 같은 과정을 거쳐 이를 해결한다.
    • successor를 선정할 때, 난수로 선택한다.
    • ΔE(변화량)이 0보다 크면 난수로 이동한다.
    • 아니면 확률적으로 난수를 선택한다. (코드에서 확률은 온도 T에 비례한다.)
     

Local Search Algorithms

• Genetic Algorithm
  • local search에서 특이하게 initial nodes 여러 개를 선택한다.
  • Fitness Function에 따라 점수와 선택 확률을 계산한다.
  • 선택 확률에 따라 부모 노드를 선택한다.
  • 선택된 두 부모 노드가 교차해 자식 노드가 생성된다.
  • 다양성을 위해 적은 수의 돌연변이가 생성된다.

유전 알고리즘 설명

Game Playing

Game

• Unpredictable하다 → Contingency plan으로 solution을 도출한다.
• 시간 제한이 있다 → 정답을 도출하기 보단 근사치를 추정한다.
• 게임의 유형은 deterministic한가, 정보가 완전한가 여부로 나뉜다.

Minimax

• deterministic & perfect-information 게임에 사용가능한 전략이다.
• 상대는 MIN 값을 선택하고, 나는 MAX값을 선택한다.
• 우측 예시에서 왼쪽 서브트리를 살펴보자.
  1. 나는 MAX인 20(2)을 선택한다.
  2. 상대는 MIN인 20(4)을 선택한다.
  3. 나는 MAX인 20(9)을 선택한다.
• 성능 측정
  • Complete: Yes
  • Optimal: Yes
  • Time Complexity: O(b^m). (분기 b의 노드를 매번 검색하기 때문)
  • Space Complexity: O(bm). (깊이 우선 탐색이기 때문)
   

게임 이론, Minmax 이론

Alpha-beta prunning

• Minimax에서 가능성이 없는 노드를 배제(가지치기)한다.
• 우측 예시에서 왼쪽 서브트리를 살펴보자.
  • 최하단에서 상대방은 MIN을 선택한다.
  • 왼쪽 서브트리에서 MAX로 20이 나왔다.
  • 그럼 오른쪽 서브트리에서 MAX가 20 이하의 값이 나와야 상대방은 MIN으로 선택한다.
  • 허나 20 이상인 30이 나왔다. 즉, 오른쪽 서브트리의 MAX는 적어도 30이다.
  • 오른쪽 서브트리는 더이상 가능성이 없으므로 11 노드를 고려하지 않는다.
• 성능 측정
  • 시간 복잡도: O(^(m/2))

알파-베타 가지치기

Minimax 심화

• Minimax에서 빠른 시간 내에 답을 하기 위해 깊이를 제한한다.
• cutoff test와 evaluation function을 사용한다.
  • evaluation function
    • features에 대한 개별 기여도를 계산해 총합을 반환한다. Q:9, L: 5, B,K: 3, P: 1
      • EVAL(Black) = 91 + 52 + 33 + 18
      • EVAL(White) = 91 + 52 + 33 + 18
      • EVAL(Black) = 91 + 52 + 33 + 18
      • EVAL(White) = 91 + 52 + 32 + 16
  • Cutting Off
    • 종료 판단이 Cutoff, 가치 및 우선순위 판단이 EVAL
    • Quiescence search이다.
    • 미래를 먼저 예측하는 것이다.

8퀸즈

MAX-Value

Nondeterministic game

• 체스와 달리 확률이 포함된 게임
• MIN노드, MAX노드, CHANCE노드로 구성된다.
• CHANCE노드에서 확률게임을 한다.

if state is a chance node then return average of EXPECTIMINIMAX-VALUE of SUCCESSORS(state)

• •  

CSP

CSP

• 제약조건을 정의해 이를 해결하는 문제이다.
• 그래프를 만들 수 있는 문제에 적합하다.
• 성능 측정
  • 공간 복잡도: n
  • 탐색 깊이: n
  • 시간 복잡도: O(|D|^2)
  • 검색 알고리즘: DFS
  • 분기 계수(branching factor):

$\Sigma i|Di|\ (at\ top\ of\ tree)$

• 다음의 두 조건으로 극적으로 향상된다
  • 할당 순서는 무관하다. 모든 경로는 비용이 같다.
  • 성능을 헤치는 constraint는 연결하지 않는다.
   

CSP

• CSP는 여러 종류가 있다.
  • Boolean
  • Binary
    • Unary
    • Binary
    • Ternary
• Binary와 Boolean은 시간이 걸리지만 풀 수 있다.
• 다만, Non-binary와 Non-boolean은 풀 수 없다.

Wumpus World

Wumpus world

8 퀸즈 문제 해결

• DFS - 가장 무식한 방식
• 백트래킹 - DFS보다 빨라졌지만 아직 느리다
• 포워드 체킹 - 미리 갈 수 없는 지역은 지우고 백트래킹 방식을 사용한다.

Arc Consistency

• 못 푸는 문제가 존재한다.
• Map Coloring with Two Colors가 그러하다 - 세 개의 지역을 두 개의 색으로 칠해야한다. 인접한 세 지역은 서로 색이 달라야한다.

Propositional

• Syntax: NOT ㄱ, AND ^, OR V, IMPLIES ⇒, IF AND ONLY IF(iff, 꼭!) <=>
• 활용: P ⇒ Q 이것은 NOT P OR Q와 같다. → 진리표를 활용해서 증명 가능.NOT(P AND Q) OR R
• NOT P OR NOT Q OR R
• (P AND Q) ⇒ R

(A OR B) AND (C OR D) —> Conjunctive Normal Form

P IFF Q = (P ⇒ Q) AND (Q ⇒ P)

 

Logic

Modus Pones

AND = conjunctive, or = disjunctive

 

Functions 와 Predicate 구별하기

• Predicate는 참, 거짓으로 구별이 된다.
  • eg. Odd(3) = 참
• Functions는 답을 도출한다.
  • add(2, 7) = 9

Term의 종류

• Constants
• Variables
• Functions